コンピュータによる情報の表し方
1.はじめに
コンピュータは数字や文字、画像や音声などの様々な情報を処理することができます。私たちは普段、電子メールやワープロソフトなどで文章を書いたり、画像を添付したり、場合によっては音声などを扱うこともあります。そのような時、私たちは文字や画像がコンピュータ内でどのような仕組みによって表されているのかということはあまり考えていません。文字や画像をコンピュータ上で自由に扱うためには、単にキーボードの配列を覚えたり、ワープロソフトの使い方に習熟すればそれで事足りると考えている人が殆どでしょう。
しかし、コンピュータを用いて知的な作業を行おうとした場合、必ずしもコンピュータの「使い方」を知っているというだけでは十分ではありません。コンピュータを自由に使いこなせるためには、単にコンピュータの使い方を覚えるだけではなく、使い方の背後にある「コンピュータの仕組み」を理解することが必要となります。これは大学に入学して間もない皆さんにとっては実感の湧かないことかもしれませんが、今後様々な授業やプロジェクトなどを通して、コンピュータの仕組みを理解することの重要性を実感していくことでしょう。そして、コンピュータの仕組みの中でも最も基礎的な事項が、ここで扱う「コンピュータによる情報の表し方」なのです。
そこで、ここではコンピュータ上で文字や画像などの情報がどのような仕組みで表現されているかということについて、できるだけ易しく解説していきます。
まず2進法と呼ばれる数字記法について説明をします。これは、コンピュータの仕組みを考える上での最も基本的な事項ですので、少し難しいかもしれませんが、頑張って理解しましょう。普段我々が日常生活で使っている数の表し方は10進位取り記法(以下10進法)と呼ばれる体系です。10進法を用いると、一桁で10個の別々のものを区別することができます。例えば、0は赤、1は青、2は緑・・・といった具合です(注1)。11個以上のものを区別するためには、桁を増やすことによって対応します。
さて、人間と違いコンピュータは2進法という表記体系を用いています。10進法に慣れ親しんだ我々からすると非常に変わった体系に思われますが、後に述べるようにコンピュータにとっては非常に都合のよい体系なのです。10進法においては0から9までの10種類の記号がありましたが、2進法には0と1の二種類しか存在しません。つまり、2進法では1桁で2種類のものしか区別することができないのです。例えば、0が男、1が女、若しくは0が偽、1が真といった具合です。3つ以上のものを区別しようとすると、桁を増やす必要があります(二進法は2の累乗で桁上がりを起こします)。ここで、2進数と10進数の対応を表にすると次のようになります(図1)。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 |
図1 2進数と10進数の対応
このように、例えば8個のもの(例えば、0から7までの数字)を区別する際に、10進法では一桁しか必要ないのに対し、2進数では三桁必要となります。また、256個のものを区別するのに、10進法では3桁あれば十分なのに対して、2進法では8桁も必要となります。随分2進法は効率が悪いと思われるかもしれませんが、電気回路であるコンピュータにとってはこちらの方が都合が良いのです。電気信号は一般にONかOFFの二通りの状態しか持たないので、ONを1、OFFを0とすると、ONとOFFの組み合わせで様々な情報を表すことができるのです。二進法を用いてコンピュータがどのように情報を表しているかについては後ほど詳しく説明をします。
コンピュータ内で表される数字や文字、画像などの情報は、必ず一定の量を持っています。「この画像ファイルは3メガバイトもある」とか「一秒間に56キロバイトの情報を送れる」、もしくは「7ビットコード表」などということを聞いたことがあるかもしれません。この時、「3メガバイト」や「7ビット」というのは「ビット」や「バイト」という単位によって情報の量を表しています。一体、情報量とはどのようなことを意味しているのでしょうか。ここでは、情報量と情報量を表す単位であるビットやバイトについて学んでいきます。
3−1 情報量の単位としてのビット、バイト
カードやコインには表と裏があるので、例えば表が黒、裏が白のカード一枚を使って、「晴れ」と「雨」の二つの天候を表すことができます。また、カードが2枚あれば「晴れ」、「雨」、「曇」、「雪」といったように4つの天候を、3枚あれば8つの天候を表すことができます(図2)。
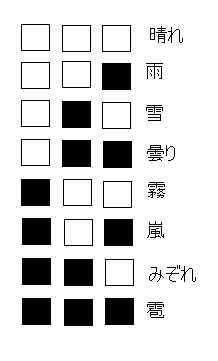
図2 カード3枚の場合
このカードを図3のように並べると、図形を表すこともできます。
さて、一枚のカードは二つの天候しか表すことができないのに対して、二枚のカードは四つの天候を表すことができますが、これは一枚のカードよりも二枚のカードの方が表すことのできる情報の量が大きいということを意味しています。三枚のカードは8つの天候を区別し、表すことができるので、二枚のカードよりも更に情報量は大きいということができます。このように、情報量とは「何種類の情報を区別し、表すことができるか」ということを意味する概念で、当然、一枚のカードより三枚のカードの方が表すことのできる情報の数が多く、情報量は大きいわけです。そして、情報量の単位として用いられるのが「ビット(語源は2進法の一桁を意味する、Binary
Digitです)」といわれるもので、一枚のカードやコインのように、二つのものを区別できるものは、「情報量1ビットをもつ」といいます。表が黒、裏が白の3枚のカードを並べると8つのものを区別し、表現することができますが(図2)、この時3枚のカードによって表現されたものは情報量としては3ビットを持つといえます。同様に、図3のように16枚のカードを並べた画像表現は16ビットの情報量をもつといえます(すなわち、2の16乗通りの異なるものを表現できるということです)。ためしに、表が黒、裏が白のカード64枚がもつ情報量をビットで表してみてください。

図3 16枚のカードによる画像表現
さて、コンピュータの内部では、全ての情報はコインやカードの表裏のかわりに1か0かの二進数によって表現されます。先ほどのカードの表裏を二進数の1、0に置き換え、8つの天候を0から7までの数に置き換えると、次のように対応づけることが出来ます(図4)。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 |
図4 2進数と10進数の対応表(図1と同じ)
この場合、8個の数を区別することのできる二進数表現(すなわち、三桁の二進数)は何ビットの情報量をもつといえるでしょうか。二つのものを区別できるもの(例えば、一枚のコイン、一枚のカード)は情報量として1ビットをもつのでした。二進数において「一枚のコイン」の「枚」にあたるのは、桁数であるといえます。一桁の二進数ならば、1か0という二つの状態の区別ができるので、1ビットの情報量をもちます。同様に、2桁ならば11、10、01、00という4つの情報を区別できるので、コインやカードで言えば2枚、すなわち2ビットの情報量をもつといえます。そうすると、0から7までの8つの数を区別するためには二進数で3桁必要なので、3ビットの情報量をもつことになります。一般に、(二進法は2の累乗で桁が増えるので)二進法ではN個のものを区別するためにLog2N桁、すなわちLog2Nビット必要であるといえます。大変わかりづらいところなので、各自図5を見てビットと桁数、区別できる情報の数の関係について確認してみて下さい。
|
10進数
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
2進数
|
0
|
1
|
10
|
11
|
100
|
101
|
110
|
111
|
|
ビット
|
1
|
1
|
2
|
2
|
3
|
3
|
3
|
3
|
図5 ビットと桁数の対応表(例えば、3つのものを区別するためには2進数で2桁、すなわち2ビット必要となる)
また、256個の情報を区別するためにはLog2256=8ビット必要ですが、一般に8ビットを1バイトと呼ぶことになっています(7ビットを1バイトとすることもあります)。さらに、1000バイトを1キロバイト、1000キロバイトを1メガバイトと呼びます。よって、「このファイルは3メガバイトもある」という表現は、「このファイルは3メガバイト=3000キロバイト=3000000バイト=24000000ビットの情報量を持つ」ということを意味しており、24000000ビットの情報量をもつとは2の24000000乗個のものを表現できるということを意味しています。カードの例で言えば、2の24000000乗個の表が黒、裏が白のカードを並べて表現されたものであるといえます。
2進法と10進法の違いについて説明しましたが、様々な局面で2進数を10進数に変換する、もしくは逆に10進数を2進数に変換する必要が出てくるときがあります。ここでは、2進数/10進数の変換方法について説明します。これはやり方さえ覚えてしまえば非常に簡単且つ有用なので、是非この機会にマスターして下さい。ちなみに、就職活動での筆記試験(SPIなど)でも頻出です。
10進数は0?9までの10個の数字を使い、10とその累乗の数(100、1000・・)で桁上がりを起こすということを思い出して下さい。そして、2進数では2とその累乗の数で桁上がりを起こします。まず、2進数を10進数に変換してみましょう。
例題1 10100011を10進数に変換しなさい
2進数は2の累乗で桁上がりを起こすので、10100011という2進数は次のように表すことができます。
|
|
上の式は、各桁に1がたっているかいないかを判断しています。1がたっている桁は2の7乗、すなわち128の位、2の5乗=32の位、2の1乗=2の位、2の0乗=1の位ということになります。10100011は、計算結果である163になります。次に、163という10進数を2進数に変換してみましょう。
例題2 10進数の163を2進数で表せ
要は今の逆を行えばよいのですが、次のような方法をとると簡単にできます。
| 2) 163 1 |
163を素因数分解の要領で2で割っていきます。その時の余りを右側に書いておきます。最後2でわれないところまできたら、下から順に余りを列挙します。この場合ですと、10100011という具合になります。これが、163を2進数に変換したものとなります。
(演習)次の2進数を10進数に、10進数を2進数に変換しなさい
(1)100100 (2)287
5−1 16進法
2進法の0と1を使ってコンピュータは様々な情報を表しています。このように、情報を表すために使用されている0と1の配列のことをビット列といいます。ビット列で情報を表す場合、情報量が増えると桁数もそれにつれて増えていきます。桁数が増えすぎると読みにくいため、ビット列を4桁ごとに区切って表現することがあります。このとき、4桁の2進数を16進数で表します(図6)。
|
10進数
|
2進数
|
16進数
|
|
0
|
0000
|
0
|
|
1
|
0001
|
1
|
|
2
|
0010
|
2
|
|
3
|
0011
|
3
|
|
4
|
0100
|
4
|
|
5
|
0101
|
5
|
|
6
|
0110
|
6
|
|
7
|
0111
|
7
|
|
8
|
1000
|
8
|
|
9
|
1001
|
9
|
|
10
|
1010
|
A
|
|
11
|
1011
|
B
|
|
12
|
1100
|
C
|
|
13
|
1101
|
D
|
|
14
|
1110
|
E
|
|
15
|
1111
|
F
|
図6 2進数 10進数 16進数の対応表
16進数は16とその累乗で桁上がりを起こしますが、0から9までの10個の数だけでは不足なので、これに加えてA〜Fの6個の英大文字を使って数を表しています。そのため、10進法の10は16進法のA、10進法の15は16進法のFとなり、10進法の16が16進法での10となります。16進数の位取りの考え方は次のようになっています。
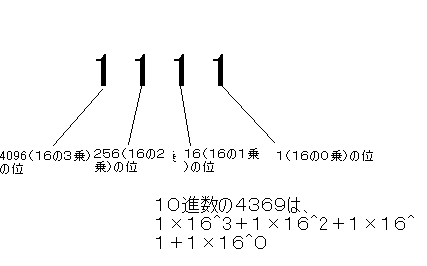
図7 16進法の位取りの考え方
5−2 2進法と16進法の変換
2進法と16進法の相互変換は次のように簡単にできます。たとえば、2進法の10011100110を16進数にする場合、以下の手順で変換します。
1. 与えられた2進数を、下の位から順に4つずつのグループに分ける。 100 1110 01102. 各グループを、対応表を基に16進数で置き換える。
3. 答え4E6
|
16進数から2進数に変換するには、これと逆の操作をすればよいわけで、16進法と2進法との変換は10進法と2進法の変換に比べてずっと簡単です。
(演習)次の2進数を16進数で表してみましょう
(2) 10101111 (2)1001001001
ここではコンピュータはどのようにして計算を行うのかということを、簡単な加算を例にとって説明します。コンピュータは2進法によって加算を行いますが、我々が普段使っている10進法と基本的な原理は同じです。試しに、3+5を二進法で加算してみます。
3は、二進法では011で表されます。また、5は、101で表されます。すると、計算は次のようになります。
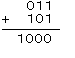
一桁目の加算で、1+1となりますが、二進法では2という記号がないため、結果は10となります。すると、10の1が桁上がりをします。次の桁は今桁上がりをした1を加えて加算を行いますが、これも同じ理屈で1+1+0=10となり、再び桁上がりを起こします。3桁目の計算も、1+0+1となり、この結果も10となり桁上がりをします。次の桁にはもう計算はないので、答えは1000となります。10進法では一桁の加算において加算結果が10以上になった場合、桁上がりを起こしますが、2進法では2以上の場合に桁上がりを起こします。
(演習)8+9を二進法で行いなさい
参考;加算回路のしくみ