HALF ADDER と FULL ADDER
1.はじめに
ここでは、コンピュータ内でのたし算の仕組みを簡単に説明します。まず、予め注意すべきことは、機械の中
では二進法で計算が進められるということです。すなわち十進法の2や3は、各々エンコーダー
という回路によって各々二進法の10,11に変換され、その上で10+11=101と二進法
の加算が行われるのです。そして、この101という答えが、デコーダーという回路によって
十進法の5に変換され、表示されることになります。しかし、今はエンコーダーやデコーダーの
回路は省略し、最も中心となる二進法の加算回路の部分についてのみ説明します。
2.Half Adder
Half Adder(半加算器)とは、一桁の加算を行う回路です。Half
Adderは、2つのものを加えるために2つの
入力部分X,Yをもつとともに、その位での和(Sum)Sと、場合によっては次の位への桁上げ分
(Carry)Cもあるゆえに、2つの出力部分S、Cをもつ回路です。Half Adderを次の図のように表します。
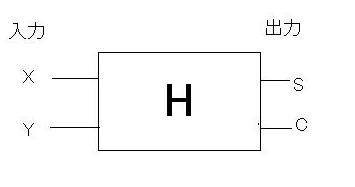
図1Half Adder
その働きは、X,Yへのあらゆる入力の場合を考えると、次の表のように表すことができます。
| X |
Y |
S |
C |
| 1 |
1 |
0 |
1 |
| 1 |
0 |
1 |
0 |
| 0 |
1 |
1 |
0 |
| 0 |
0 |
0 |
0 |
表1 X、Y、S、Cの入出力表
このようにしてみると、S,Cは真理関数であり、この表は真理値表としてみることができます。
Cは連言X∧Yを表しています。
Sは排他的選言(Exclusive Or)と呼ばれ、通常の選言とは
異なります。通常の選言X∨Yは、X,Yが共に1の場合、真とされます。これは例えば、
「A鉄道がストか、B鉄道がストの場合、学校は休講になる」と言った時に、両鉄道ともにストだった
場合にも学校が休講になるということを表します。しかし、排他的選言は、例えば「お茶またはコー
ヒーをどうぞ」と言った場合、両方を選択することができないように、X,Yがともに1の場合は偽
とみなされます。なお論理式は(X∧¬Y)∨(¬X∧Y)となります(注1参照)。
一般に、論理式にはそれに対応するような電気的回路が存在します。というのは、
論理式は∧、∨、¬という結合子からできているわけですが、その各々についてその真理値表を
表しているような電気的回路が考えられるからです。したがって、そうした回路を論理式に
即して組み合わせていけば、論理式に対応する回路も容易につくることができます。そこでまず図2
に、∧に対応するAND回路、∨に対応するOR回路、¬に対応するNOT回路の原理図を示します。
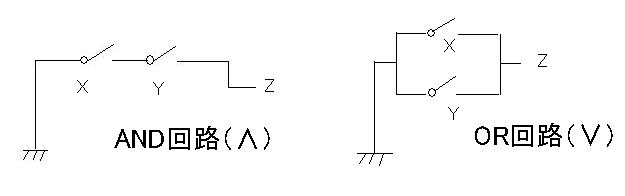
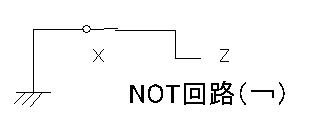
図2 論理回路
AND回路では、Xに入力すると電磁石が働いてそこのスイッチが閉じ、さらにYにも入力すると同様にそこのスイッチが閉じます。スイッチは直列なので、そのとき初めて、出力のZに電流が流れます。OR回路のスイッチは並列になっているので、XかYに入力すれば、Zに電流が流れます。また、NOT回路の場合には逆に、Xに入力するとスイッチが開き、Zに電流が流れなくなります。
これらを利用して、Half Adderの回路を表すと、次のようになります。Eで表されているのはExclusive Or、つまり、(X∧¬Y)∨(¬X∧Y)の回路ですが、中身は省略しています。
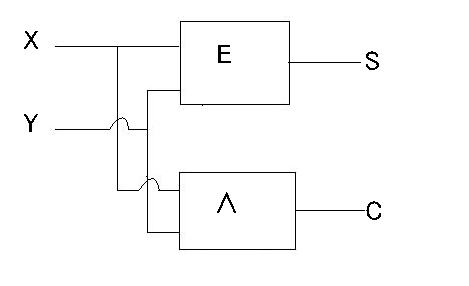
図3 Half Adderの回路
この回路によって、一桁の加算を行うことができるようになりました。
3.Full Adder
Half Adderだけでは、一桁の加算しか行うことができません。そこで、一般の位を計算する回路
をつくってみましょう。一般の位というのは、例えば2桁目でもよいし、3桁目でもよいということ
です。ここで注意することは、一般の位の計算では、前の桁からの桁上がり(C)が含まれるという
ことです。たとえば、二進法の111+011を考えてみましょう。
111
+ 011
----------
二桁目を計算しようとするとき、単に1+1を考えるだけではだめで、一桁目の桁上がりの1
も加算しなくてはなりません(Half Adderでは、この点が考慮されていません)。すなわち、1+1+1が
二桁目でなされるべき計算になります。そこで、Full Adderでは、計算する入力部分として、X,Yに加え、
前の桁からの桁上がりC’の3つをもつことになります。そして、出力はその桁の和S(この場合では、
1+1+1=11なので、一桁目の1がSとなります)と桁上がりするC(この場合では1+1+1=11の
二桁目の1)となります。これを、上と同様の表で表すと次のようになります。
| X |
Y |
C |
S |
C' |
| 1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
0 |
1 |
| 1 |
0 |
0 |
1 |
0 |
| 0 |
1 |
1 |
0 |
1 |
| 0 |
1 |
0 |
1 |
0 |
| 0 |
0 |
1 |
1 |
0 |
| 0 |
0 |
0 |
0 |
0 |
表2 X、Y、C、S、C' の入出力表
また、Full Adderは次のように表します。
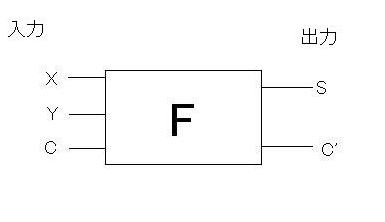
図4 Full Adder
さて、実際にFull Adderはどのような回路になるのでしょうか。次図がFull Adderを表した回路です。
中にHalf Adderが埋め込まれているのがわかります。
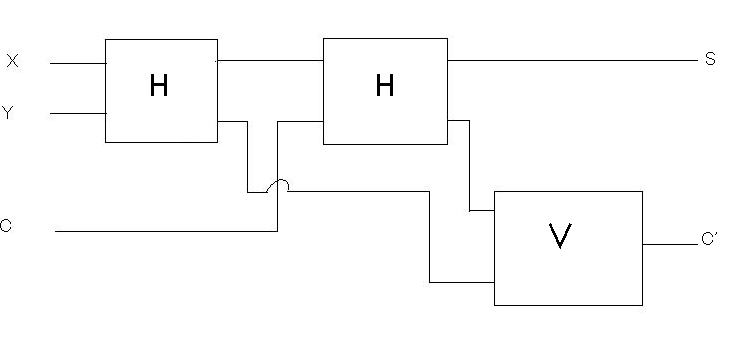
図5 Full Adderの回路
この回路を用いると、一般の位についての加算を行うことができます。ここでは、111+011の二桁目の計算を見てみましょう。111+011の二桁目の計算は1+1に加え、一桁目の桁上がりである1を加えなければなりません。
そこで、入力部分X,Yにはそれぞれ1が、C(前の桁からの桁上がり)にも1が入ります。
一つ目のHalf Adderの出力は、Sが0、Cが1となります(先の真理値表を見れば、X,Yがともに
1の場合は、Sは0、Cは1です)。二つ目のHalf Adderの入力は、0と1になり、その出力は真理値表
から1、0となります。1はそのままFull Adderの出力となり、一つ目のHalf Adderと二つ目のHalf Adder
の桁上がりがOR回路を通り、Full Adderの出力C’となります。ここで、C’は次の桁への桁上がり
なので、Full Adderを3つつなげれば2桁の加算を行うことができます。
以上のように、最初の位、一般の位を計算する回路ができたので、後はFull Adderを連結すれば、二進法の加算を行う回路が完成します。
次の図は、2+3、すなわち
10+11を加算する例を示しています。
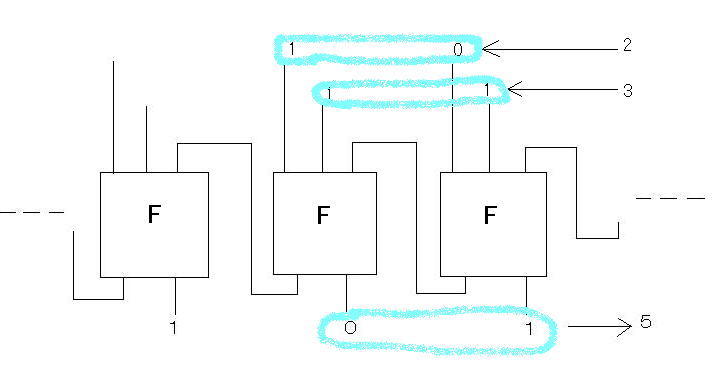
図6 加算回路